文章目录

GAMES101-现代图形学入门笔记7-9：着色、纹理

该课程是 GAMES 开设的现代计算机图形学课程，系统而全面的介绍：光栅化、几何表示、光的传播理论、动画与模拟。每个方面都从基础原理出发讲解到实际应用，并介绍前沿的理论研究。本文是其 7、8、9 章着色和纹理的学习笔记。

1. 着色

着色定义

绘画着色定义：The darkening or coloring of an illustration or diagram with parallel lines or a block of color。

本课程的定义：对不同物体应用不同材质的操作（The process of applying a material to an object）。

简单的着色模型

知觉观察：

高光（Specular highlights）
漫反射（Diffuse reflection）
间接光照（Ambient lighting）

局部着色

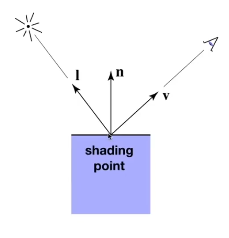
假设：假设着色发生在着色点，在着色点附近的极小区域可以视为平面。

输入，方向都设为单位向量：

观察者方向 $\vec{v}$
表面法线 $\vec{n}$
光线方向 $\vec{l}$ ，对于很多不同的光线
表面参数：
- 颜色
- 光泽度
- ……

考虑任何点的着色都只看自身，而不看其它物体的存在 —— 并不生成阴影。

漫反射（Diffuse Reflection）

光线接受

光线被均匀地反射（scattered）反射到所有方向上去。

表面朝向、光线角度和最终效果有关，接受到的光线与入射光线和法线夹角正比 —— 兰伯特余弦定则：

l_{received} = \vec{l} \cdot \vec{n} \tag {1}

能量衰减

能量衰减：理想空间中均匀传递出的球壳能量完全相同，因此有：

I_f \cdot \pi d_f^2= I_n \cdot \pi d_n^2 \tag {2}

Lambertian（Diffuse）Shading

反射独立于视角方向。

L_d = k_d\frac{I}{r^2}\max(0, \vec{n}\cdot\vec{l}) \tag{3}

其中， $L_d$ 是漫反射的光线； $k_d$ 是漫反射系数（该值与颜色相关）； $\frac{I}{r^2}$ 代表到达着色点的光线； $\max(0, \vec{n}\cdot\vec{l})$ 代表被着色点吸收的系数。

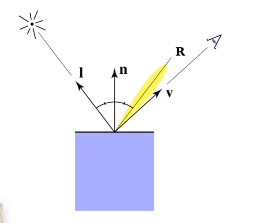
高光（Specular）

Blinn-Phong 高光项

高光项强度依赖于视角方向：接近镜面反射的方向。

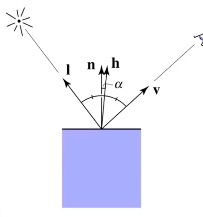
观察：当 $\vec{v}$ 接近镜面反射方向的时候，说明了法线和半程向量接近 —— 通过点乘测量单位向量可以测量“接近”。

\begin{aligned} \vec{h} &= bisector(\vec{v}, \vec{l}) \\ &= \frac{\vec{v} + \vec{l}}{||\vec{v} + \vec{l}||} \end{aligned} \tag{4}

其中， $\vec{h}$ 表示半程向量。则高光可以通过以下公式计算：

\begin{aligned} L_s &= k_s\frac{I}{r^2}\max(0, \cos{\alpha})^p \\ &= k_s\frac{I}{r^2}\max(0, \vec{n}\cdot\vec{h})^p \end{aligned} \tag{5}

其中： $k_s$ 代表光泽度； $p$ 项用来减小高光的范围（易想到高光只出现在极小的范围），一般用 100-200 的系数。

间接光照（Ambient）

环境光着色并不依赖任何其他：

添加常数颜色来保证没有地方是黑的并提升一个亮度
环境光与实际的直接光照没有关系
与观测方向无关
这是一个及其大胆的非真实假设，想要真正地计算它，需要全局光照

L_a = k_a L_a \tag{6}

Blinn-Phong 反射模型

Blinn-Phong Reflection = Ambient + Diffuse + Specular

\begin{aligned} L &= L_a + L_d + L_s \\ &= k_a I_a + k_d\frac{I}{r^2}\max(0, \vec{n}\cdot\vec{l}) + k_s\frac{I}{r^2}\max(0, \vec{n}\cdot\vec{h})^p \end {aligned} \tag{7}

着色频率

三种直观的着色频率：

面着色
顶点着色：三角形内部进行差值
像素着色

当几何相对复杂的情况下（比如面特别多），简单的着色频率效果不一定差，成本不一定低。

平面着色（flat shading）

平面着色：着色每个三角形

三角形的面是一个平面，拥有一个法向量
对于平滑表面效果不好

顶点着色（Gouraud shading）

顶点着色：

每个顶点进行着色，三角形内部对顶点颜色进行插值
每个顶点拥有一个法线

像素着色（Phong Shading）

像素着色：

对三角形的三个顶点求出各自的法线，对内部的每个像素插值出其法线
对每个像素计算一次全着色模型
不是 Blinn-Phong 反射模型

顶点法线和像素法线

顶点法线

观察：任何一个顶点都和很多个面相关联。

方法：

使用相邻的法线求平均
使用相邻的三角形的法线和其面积求加权平均

像素法线

见后续中心坐标部分

2. 管线

管线流程

图形管线：本课程指实时渲染管线。

如何从应用到显示：

Input: vertices in 3D space
Vertex Stream: Vertices positioned in screen space
Triangle Stream: Triangles positioned in screen space
Fragment Stream: Fragments, on per covered sample
Shaded Fragments
Output: Image (pixels)

着色器简介

编程顶点和片段处理步骤
描述对于单个顶点和片段的操作

示例 GLSL 片段着色器程序如下：

uniform sampler2D myTexture;
uniform vec3 lightDir;
varying vec2 uv;
varying vec3 norm;

void diffuseShader() {
    vec3 kd;
    kd = texture2D(myTexture, uv);
    kd *= clamp(dot(-lightDir, norm), 0.0, 1.0);
    gl_FragColor = vec4(kd, 1.0);
}

uniform sampler2D myTexture;

uniform vec3 lightDir;

varying vec2 uv;

varying vec3 norm;

void diffuseShader() {

vec3 kd;

kd = texture2D(myTexture, uv);

kd *= clamp(dot(-lightDir, norm), 0.0, 1.0);

gl_FragColor = vec4(kd, 1.0);

}

上述着色器：

着色器函数对于每个片段执行
输出当前片段的银幕采样位置的表面颜色

推荐网站：

shadertoy

拓展

通过 shader 可以实现相当多复杂的功能
游戏引擎集成了相当多的现成工具
越来越多的着色器：
- 几何 shader：动态产生三角形
- 计算 shader：可以完成复杂的计算，GPGPU
GPU 并行度非常高

3. 纹理映射和进阶

纹理映射

目的

希望有一种方法能够定义物体的任何一个点上的属性。

方法和定义

任何一个物体的表面都是 2D 的
对于多个物体可以分成多张图：拉伸、压缩、包围、分割

纹理上的坐标

每个三角形顶点能够被赋予一个顶点坐标： $(u,v)$ ：

为方便处理，认为 $u$ 、 $v$ 的范围都在 $[0,1]$
不同位置的纹理可以映射到同一个位置
纹理设计时要考虑重复的衔接问题，这种设计称为 tilable

重心坐标（Barycentric Coordinates）

重心坐标：三角形插值

三角形插值

为何在三角形中插值？

在三角形中获得平滑变化的值
指明顶点的值

插值的内容？

材质轴、颜色、法线向量等

如何插值：

重心坐标

重心坐标

重心坐标是定义在三角形上的坐标系系统 $(\alpha, \beta, \gamma)$

\begin{aligned} (x, y) = &\alpha A + \beta B + \gamma C \\ &\alpha + \beta + \gamma = 1 \end{aligned} \tag{8}

三角形内的任何一个点都可以使用三个顶点的线性组合即可，需满足系数之和为 1。

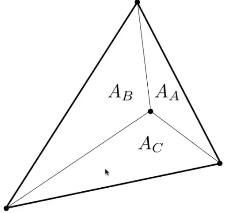
实际上由于这种限制，只需要两个值就可以表示。三个值都需要非负，才能表示该值位于三角形内部。

\begin{aligned} \alpha &= \frac{A_A}{A_A + A_B + A_C} \\ \beta &= \frac{A_B}{A_A + A_B + A_C} \\ \gamma &= \frac{A_C}{A_A + A_B + A_C} \end{aligned} \tag{9}

通过以上方法，可得三角形重心为：

\begin{aligned} (\alpha, \beta, \gamma) &= (\frac{1}{3}, \frac{1}{3},\frac{1}{3}) \\ (x, y) &= \frac{1}{3} A + \frac{1}{3} B + \frac{1}{3} C \end{aligned} \tag{10}

通用的坐标向重心坐标的转换得：

\begin{aligned} \alpha &= \frac{-(x-x_B)(y_C-y_B) + (y-y_B)(x_C-X_B)}{-(x_A – x_B)(y_C – y_B) + (y_A – y_B)(x_C – x_B)} \\ \beta &= \frac{-(x-x_C)(y_A-y_C) + (y-y_C)(x_A-X_C)}{-(x_B – x_C)(y_A – y_C) + (y_B – y_C)(x_A – x_C)} \\ \gamma &= 1 – \alpha – \beta \end{aligned} \tag{11}

可以使用重心坐标来做三角形内部属性的插值，插值的属性同样应该使用中心坐标来线性的组合出来：

V = \alpha V_A + \beta V_B + \gamma V_C \tag{12}

在投影变化下不能保证重心坐标不变，因此在三维下取坐标应该在三维坐标系中取，而不能在投影之后的结果中取。

纹理过滤

简单纹理映射：散射颜色

伪代码如下：

for each rasterized screen sample (x,y):
    (u, v) = evaluate texture coordinate at (x,y);
    texcolor = texture.sample(u,v);
    set sample's color to texcolor;

for each rasterized screen sample (x,y):

(u, v) = evaluate texture coordinate at (x,y);

texcolor = texture.sample(u,v);

set sample's color to texcolor;

其中，纹理坐标使用重心坐标，通常 color 指的是 diffuse albedo $k_d$ 。

纹理放大 – 双线性插值

纹理放大（Texture Magnification）：如果纹理太小了？

Neareast 邻近插值：Round(val)
Bilinear 双线性插值：
1. 获取邻近的四个点
2. 获得离左下角的水平距离和竖直距离 $(s,t), s、t \in [0,1]$
3. 定义线性插值： $lerp(x, v_0, v_1) = v_0 + x(v_1 - v_0)$
4. 进行线性插值：
  - $u_0 = lerp(s, v_{00}, u_{10})$
  - $u_1 = lerp(s, u_{01}, u_{11})$
  - $f(x,y) = lerp(t, u_0, u_1)$
Bicubic 双向三次插值：
1. 取邻近 16 个点
2. 4 个成组进行插值
3. 4 组插值结果分别进行插值

PS：A pixel on a texture – a texel

好的质量往往伴随着更大开销

纹理过大 – 三线性插值（Trilinear）

仍然是走样的问题。

简单的修正方法？MSAA：太慢

另一个思路：

采样会引起走样 => 不查询
点查询 => 范围查询

Mipmap：允许进行范围查询，快速、近似、方形，它可以从一张图生成更多的纹理（计算机视觉称为图像金字塔），占据的空间为 4/3。

计算 Mipmap 等级 D：

\begin{aligned} D &= \log_2{L} \\ L &= \max{ \left( \sqrt{(\frac{du}{dx})^2 + (\frac{dv}{dx})^2} \cdot \sqrt{(\frac{du}{dy})^2 + (\frac{dv}{dy})^2} \right) } \end{aligned} \tag{13}

思路是将右方和上方的点投影到材质上，计算近似距离；可以看做求微分。查询在第几层是 1 个像素的值。

不希望在不连续的层上查询，则可以进行对不同层上的结果进行插值 – 三线性插值。

Mipmap 局限性 – 各向异性过滤（Anisotropic）

远处过模糊？Mipmap 只能进行正方形过滤

Ripmaps 和 summed area 表：

可以查询矩形压缩
但是仍然不能解决斜向问题
总共的开销是原本的三倍
nX 各项异性过滤代表压缩到多少倍，和显卡性能基本无关，基本只和显存有关

其他过滤方法 – EWA

EWA 过滤：

有任意不规则形状，可以拆成很多圆形来覆盖区域，多次查询覆盖圆形
代价较高